Special LCS

Special coordinate systems as well as workplanes are intended for setting three-dimensional elements and their correct location in space. As surfaces that can be used to define a special coordinate systems are supported by the cylinder, the sphere and the torus. This method of defining geometry is often used when building complex surfaces, such as when designing propellers. The essence of the method is that a flat image, for example, a hatching profile, is located on a cylinder, sphere, or torus by means of transformation. To bind special coordinate systems in space, the local coordinate system is used.

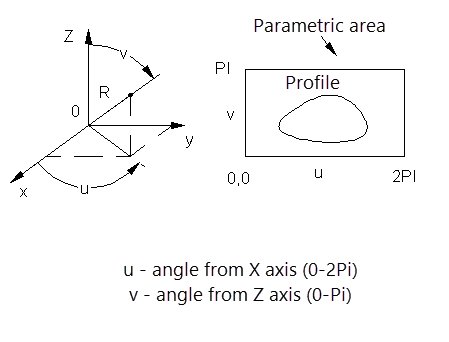
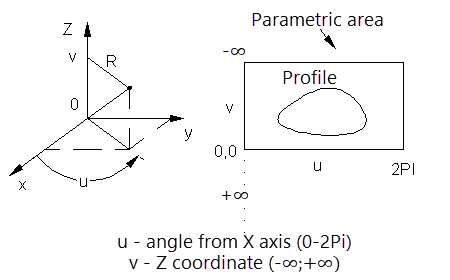
Special coordinate systems are defined within a parametric area that represents the "sweep" of a surface onto a plane. The parametric area is defined in u and v coordinates. The range of coordinate changes and the meaning attached to the coordinates depend on the type of surface used to set the special coordinate system.

Spherical coordinate system

Cylindrical coordinate system

Toroidal coordinate system

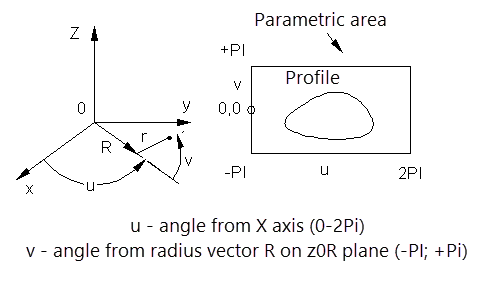
R-radius of a cylinder, sphere, or large radius of a torus

r - small radius of the torus

Parametric regions of spherical and toroidal coordinate systems have restrictions from the bottom and top. Cylindrical vertical coordinate systems are not restricted. In addition, cylindrical coordinate systems can be set in either angular or linear units.