Combined Usage of Fixing by LCS and Mates

In this section, we review the recommended rules of combined usage of mates and fixing by LCS, when creating assemblies. Fixing parts by mates shall mainly be used together with fixing by LCS. Note also that priority shall be given to the traditional way – fixing fragments by coordinate systems. This approach has a number of advantages over mates.

Firstly, some types of geometrical relations, including the most commonly used (as a single-axis joint), can be solved by one LCS, while in the mate approach it may require bundling two or more mates. In particular, a single-axis joint is defined by two mates (concentricity + coincidence of end faces), or just one LCS (with rotation allowed about one axis). This main advantage has more consequences:

•Overall, the system works faster (the chain of mates becomes shorter, computational errors are reduced, calculations become simpler).

•A simpler model structure results from avoiding extra elements (the mates).

•The model becomes more robust to topological changes (due to minimized use of topological body elements).

So then, when the use of mates is justified? To answer this question, let's review the process of designing an assembly. In regard to the posed question, the designer typically faces 2 tasks.

Task 1

Creating an assembly model without the possibility of "movement" of the mechanism. The user knows in advance that he is designing, that his model will not have to move after the assembly is completed, he does not need it. For example, if we are designing a TV or a house, it is unlikely that we will need to "revive" them in dynamic mode.

When the user is faced with a similar task, when filling the assembly with parts, one main question is solved – how to correctly position the part on the assembly. The most effective solution is provided by the "traditional" method – inserting 3D fragments using LCS. In addition to the general advantages of this method, fewer actions will be required from the user. The 3D fragment insertion mechanism requires less time due to the fact that fewer elements need to be defined:

1. The source LCS (selection can be performed automatically).

2. The location of the binding (the choice of the target LCS or geometry for its creation is carried out in the 3D window).

At the same time, each new mate would require the definition of geometric data for two components, and for the exact location of the component, as a rule, you need to create several mates.

It is necessary to resort to the use of mates:

•in complex cases of geometric interaction;

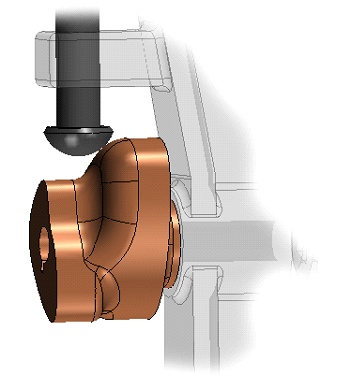
•when it is required to place a part on the assembly that has contact with other parts in several places.

Task 2

Building an assembly with the possibility of "reviving" the designed mechanism in the command of moving the mated elements. In this case, all parts of the assembled mechanism must interact correctly with each other. For all moving parts, the necessary conditions for calculating the coupling system during the movement of the mechanism must be described.

In this situation, it is recommended to follow the rules given below.

•For parts that should not change their position relative to the elements to which they are attached, it is recommended to use a LCS without degrees of freedom. For example, a nut placed on a bolt should always follow the bolt and should not have movements relative to the bolt.

•For parts that change the mutual position, first of all you need to use a LCS with degrees of freedom. This will give a win for all the main advantages (see above).

Mates are used when binding parts in the following cases:

•For parts that have complex geometric interactions.

•For parts that have more than one contact with several moving adjacent parts.

•To close the mated chains. At the same time, each chain can be created using LCS with degrees of freedom.

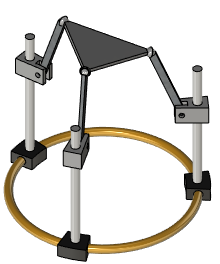
The platform is paired with three adjacent parts. Three chains of mates are closed

•To set various restrictions, for example, on the mutual penetration of parts. As an example, we can consider a hydraulic cylinder, where restrictions are set in the form of the condition "distance =0" (see the Types of Mates section).